Luas Tabung Tanpa Tutup

Cara Memperoleh Rumus Cepat Luas Ember Tanpa Tutup House

Rumus Menghitung Luas Permukaan Tabung Tanpa Tutup Dan Contoh Soalnya

Homepage / Matematika / Rumus Menghitung Luas Permukaan Tabung Tanpa Tutup Dan Contoh Soalnya

Rumus Menghitung Luas Permukaan Tabung Tanpa Tutup Dan Contoh Soalnya – Pada pembahasan kali ini kita akan jelaskan materi tentang bagaimana rumus menghitung luas permukaan tabung tanpa tututp berikut contoh soalnya.

Mari langsung saja kita simak!

Rumus luas Permukaan Tabung Tanpa Tutup

Luas Permukaan Tabung

Luas permukaan tabung adalah suatu luas dari beberapa jumlah sisi yang dimiliki oleh tabung. Jumlah sisi suatu tabung sama dengan bidang pembentuk tabung. Bidang pembentuknya tersebut ada  yaitu terdiri dari dua buah lingkaran yang menjadi alas dan tutupnya, serta satu buah selimut tabung yang berbentuk persegi panjang. Luas permukaan ini memiliki pengaruh terhadap besar dan kecilnya suatu tabung.

Luas Permukaan Tanpa Tutup Tabung

Luas permukaan tabung tanpa tutup adalah suatu luas permukaan yang hampir sama dengan luas permukaan tabung, hanya bedanya dari segi tutupnya saja, luas permukaan tanpa tutup tabung ini tidak ada tutupnya. Oleh karena tidak ada tutupnya, maka luas sisi tutup tabung yang berupa lingkaran tersebut tidak dihitung.

Gambar 1

Gambar 2

Jadi jika tabung tanpa tutup maka gambarnya kurang lebih sebagai berikut:

Gambar 1

Gambar 2

Rumus Luas Permukaan Tabung Tanpa Tutup

Untuk menghitung luas permukaan tabung tanpa tutup, maka kita dapat menggunakan rumusnya sebagai berikut:

L. tabung tanpa tutup = π x r² + 2 x π x r x t = π x r (r + 2t)

Demikianlah rumusnya, sekarang kita lanjutkan ke contoh soal dan pembahasannya.

Contoh Soal Dan Pembahasan

Soal 1: Diketahui sebuah tabung berdiameter 10 cm dengan tinggi tabung adalah 26 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?

Pembahasan: L. permukaan tabung tanpa tutup = π x r (r + 2t)

L. permukaan tabung tanpa tutup = 3,14 x 5 x (5 x 2 x 26)

L. permukaan tabung tanpa tutup = 3,14 x 5 x (5 x 52) L. permukaan tabung tanpa tutup = 3,14 x 5 x 57

L. permukaan tabung tanpa tutup = 894,9 cm²

Jadi, luas permukaan tabung tanpa tutup tersebut adalah 894,9 cm²

Soal 2: Diketahui sebuah tabung berdiameter 16 cm dengan tinggi tabung adalah 28 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?

Baca Juga :   Rumus dan Cara Menentukan Persamaan Garis Lurus

Pembahasan: L. permukaan tabung tanpa tutup = π x r (r + 2t)

L. permukaan tabung tanpa tutup = 3,14 x 14 x (14 x 2 x 28)

L. permukaan tabung tanpa tutup = 3,14 x 14 x (14 x 56) L. permukaan tabung tanpa tutup = 3,14 x 14 x 784

L. permukaan tabung tanpa tutup = 34.464,94 cm²

Jadi, luas permukaan tabung tanpa tutup tersebut adalah 34.464,94 cm²

Soal 3: Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 24 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?

Pembahasan: L. permukaan tabung tanpa tutup = π x r (r + 2t)

L. permukaan tabung tanpa tutup = 3,14 x 10 x (10 x 2 x 24)

L. permukaan tabung tanpa tutup = 3,14 x 10 x (10 x 48) L. permukaan tabung tanpa tutup = 3,14 x 10 x 480

L. permukaan tabung tanpa tutup = 15.072 cm²

Jadi, luas permukaan tabung tanpa tutup tersebut adalah 15.072 cm²

Soal 4: Diketahui sebuah tabung berdiameter 30 cm dengan tinggi tabung adalah 36 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?

Pembahasan: L. permukaan tabung tanpa tutup = π x r (r + 2t)

L. permukaan tabung tanpa tutup = 3,14 x 15 x (15 x 2 x 36)

L. permukaan tabung tanpa tutup = 3,14 x 15 x (15 x 72) L. permukaan tabung tanpa tutup = 3,14 x 15 x 72

L. permukaan tabung tanpa tutup = 3.391,2 cm²

Jadi, luas permukaan tabung tanpa tutup tersebut adalah 3.391,2 cm²

Soal 5: Diketahui sebuah tabung berdiameter 46 cm dengan tinggi tabung adalah 56 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?

Pembahasan: L. permukaan tabung tanpa tutup = π x r (r + 2t)

L. permukaan tabung tanpa tutup = 3,14 x 23 x (23 x 2 x 56)

L. permukaan tabung tanpa tutup = 3,14 x 23 x (23 x 112) L. permukaan tabung tanpa tutup = 3,14 x 23 x 57

L. permukaan tabung tanpa tutup = 87.584 cm²

Jadi, luas permukaan tabung tanpa tutup tersebut adalah 87.584 cm²

Baca Juga:

Rumus Menghitung Luas Permukaan Tabung Tanpa Tutup Dan Contoh Soalnya 02/09/2019 2:49:52 PM Rating: 5 Diposkan Oleh: Pelajar

Gallery Luas Tabung Tanpa Tutup

Doc Sebuah Tabung Memilliki Jari Jari 3 Rahayu Nigsih

No 22 Aplikasi Turunan Tabung Tanpa Tutup Un 2017 Paket2 Sma Ipa Matematika Soal Dan Pembahasan

Ppt Luas Permukaan Tabung Kelas Viii Smp

Rumus Menghitung Luas Permukaan Tabung Tanpa Tutup Dan

Cara Menghitung Rumus Luas Permukaan Dan Volume Tabung

Un Sma 2017 Matematika Ipa Pembahasan No 24 Jari Jari Agar Luas Permukaan Minimum

Sebuah Tabung Tanpa Tutup Mempunyai Jari Jari Alas 6 Cm Dan

Mencari Luar Permukaan Tabung Tanpa Tutup Dan Dengan Tutup

Hitunglah Luas Permukaan Masing Masing Tabung Tanpa Tutup

Diana Agustin S Maret 2016

Volume Tabung Rumus Contoh Luas Dan Cara Menghitungnya

Rumus Rolling Pipa Xinhai

Rumus Luas Permukaan Tabung Dan Rumus Luas Selimut Tabung

01 Ebtanas Smp Volume Sebuah Kerucut Adalah 314 Cm3 Jika

Soal Ulangan Harian Bangun Ruang Sisi Lengkung Docx Document

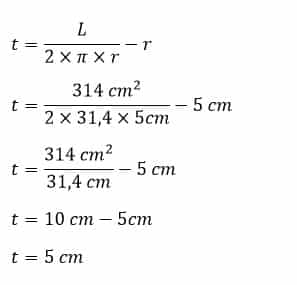Rumus Volume Tabung Luas Permukaan Tinggi Dan Contoh Soal

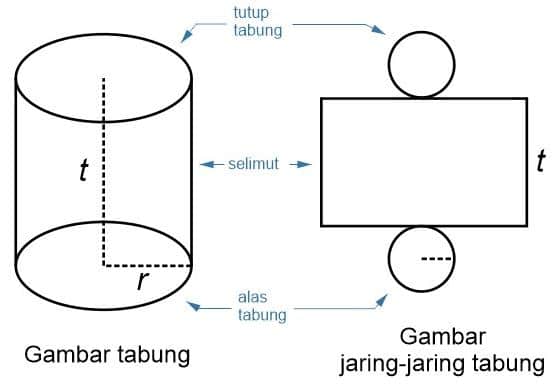Rumus Tabung Volume Luas Permukaan Keliling Tinggi Dan

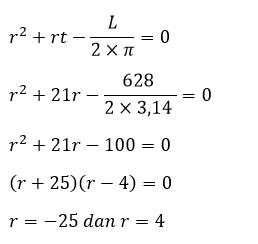Rumus Tabung Volume Luas Permukaan Keliling Tinggi Dan

Rumus Luas Permukaan Tabung Dan Rumus Luas Selimut Tabung

Bangun Ruang Sisi Lengkung

Soal Bangun Ruang Sisi Lengkung

Rumus Luas Tabung Pojok Menulis