 Tabel Kebenaran Dari Gerbang Nor Zona Elektro
Tabel Kebenaran Dari Gerbang Nor Zona Elektro
Materi Dasar Logika Informatika [Tabel kebenaran]

Logika dan Pernyataan | |
1. Logika | |
2. Pernyataan (Proposisi) | |
3. Penghubung Kalimat Dan Tabel Kebenaran | |
4. Ingkaran (Negasi) Suatu Pernyataan,Konjungsi,Disjungsi dan implikasi. 5. Invers,konvers,dan kontraposisi | |
- Premis : yaitu sebuah pernyataan
- Argumen : usaha untuk mencari kebenaran dari premis berupa kesimpulan
- Konklusi : Kesimpulan
2. PERNYATAAN (PROPOSISI)
Kata merupakan rangkaian huruf yang mengandung arti, sedangkan kalimat adalah kumpulan kata yang disusun menurut aturan tata bahasa dan mengandung arti. Di dalam matematika tidak semua pernyataan yang bernilai benar atau salah saja yang digunakan dalam penalaran. Pernyataan disebut juga kalimat deklaratif yaitu kalimat yang bersifat menerangkan. Disebut juga proposisi.
Pernyataan/ Kalimat Deklaratif/ Proposisi adalah kalimat yang bernilai benar atau salah tetapi tidak keduanya.
Contoh :
- Yogyakarta adalah kota pelajar (Benar).
- 2+2=4 (Benar).
Tidak semua kalimat berupa proposisi
Contoh :
- Dimanakah letak pulau bali?.
- Pandaikah dia?.
#penalaran deduktif
penalaran yang didasarkan premis-premis yang diandaikan benar untuk menarik kesimpulan.
contoh:
1. semua mahasiswa baru mengikuti ospek.
2. wulandari adalah mahasiswa baru.
kesimpulannya : wulandari mengikut ospek.
#penalaran induktif
penalaran yang didasarkan pada premis-premis yang bersifat faktual untuk menarik kesimpulan yang bersifat umum.
contoh:
premis 1 : ayam 1 berkembang biak dengan telur
premis 2 : ayam 2 berkembang biak dengan telur
premis 3 : ayam 3 berkembang biak dengan telur
...
...
...
premis 50 : ayam 50 berkembang biak dengan telur
kesimpulannya : semua ayam berkembang biak dengan telur
Pernyataan:
- Pernyataan adalah kalimat yang mempunyai nilai kebenaran (salah/benar)
- Pernyataan yang tidak mengandung kata hubung kalimat,disebut pernyataan primer/tunggal/atom. Sedangkan pernyataan yang mengandung satu atau lebih kata hubung kalimat,disebut pernyataan majemuk.
3. PENGHUBUNG KALIMAT DAN TABEL KEBENARAN
KATA HUBUNG KALIMAT
Simbol | Arti | Bentuk |
| ¬/~ | Tidak/Not/Negasi | Tidak…………. |
| ^ | Dan/And/Konjungsi | ……..dan…….. |
| v | Atau/Or/Disjungsi | ………atau……. |
| => | Implikasi | Jika…….maka……. |
| < => | Bi-Implikasi | ……..bila dan hanya bila…….. |
TABEL KEBENARAN
p | q | ~p | ~q | p^q | pvq | p=>q | p <=>q | |
B | B | S | S | B | B | S | B | |
B | S | S | B | S | B | B | S | |
S | B | B | S | S | B | B | B | |
S | S | B | B | S | S | S | B |
A. NEGASI (INGKARAN)
Contoh:
a. p: semua siswa punya almamater ~ p : beberapa siswa tidak punya almamaterb. q : uki anak yang pandai
~ q : uki bukan anak yang pandaiB. KONJUNGSI
Konjungsi adalah suatu pernyataan majemuk yang menggunakan penghubung “DAN/AND” dengan notasi “^”
Contoh:
a. p: Fahmi makan nasi
q:Fahmi minum kopi
Maka p^q : Fahmi makan nasi dan minum kopi b. p: Aan anak yang pemalas q: Aan anak yang ngantukan Maka p^q : Aan anak yang pemalas dan ngantukan
Pada konjungsi p^q akan bernilai benar jika baik p maupun q bernilai benar. Jika salah satunya (atau keduanya) bernilai salah maka pÙq bernilai salah.
C. DISJUNGSI
Disjungsi adalah pernyataan majemuk yang menggunakan penghubung “ATAU/OR” dengan notasi “v”.
Kalimat disjungsi dapat mempunyai 2 arti yaitu :
a. INKLUSIF OR
Yaitu jika “p benar atau q benar atau keduanya true”
Contoh :
p : 7 adalah bilangan prima
q : 7 adalah bilangan ganjil
p v q : 7 adalah bilangan prima atau ganjil
Benar bahwa 7 bisa dikatakan bilangan prima sekaligus bilangan ganjil.
b. EKSLUSIF OR
Yaitu jika “p benar atau q benar tetapi tidak keduanya”.
Contoh :
p : Saya akan melihat pertandingan bola di TV.
q : Saya akan melihat pertandingan bola di lapangan.
p v q : Saya akan melihat pertandingan bola di TV atau lapangan.
Hanya salah satu dari 2 kalimat penyusunnya yang boleh bernilai benar yaitu jika “Saya akan melihat pertandingan sepak bola di TV saja atau di lapangan saja tetapi tidak keduanya.
D. IMPLIKASI
Misalkan ada 2 pernyataan p dan q, untuk menunjukkan atau membuktikan bahwa jika p bernilai benar akan menjadikan q bernilai benar juga, diletakkan kata “JIKA” sebelum pernyataan pertama lalu diletakkan kata “MAKA” sebelum pernyataan kedua sehingga didapatkan suatu pernyataan majemuk yang disebut dengan “IMPLIKASI/PERNYATAAN BERSYARAT/KONDISIONAL/ HYPOTHETICAL dengan notasi “ =>”.
Notasi pÞq dapat dibaca :
- Jika p maka q
- q jika p
- p adalah syarat cukup untuk q
- q adalah syarat perlu untuk p
q : Pak Ali adalah seorang muslim.
p => q : Jika Pak Ali adalah seorang haji maka pastilah dia seorang muslim. 2. p : Hari hujan. q : Adi membawa payung.Benar atau salahkah pernyataan berikut? a. Hari benar-benar hujan dan Adi benar-benar membawa payung. b. Hari benar-benar hujan tetapi Adi tidak membawa payung. c. Hari tidak hujan tetapi Adi membawa payung. d. Hari tidak hujan dan Adi tidak membawa payung.
1.1 KONVERS, INVERS, DAN KONTRAPOSISI
Perhatikan pernytaan di bawah ini! ~ ^ v => <=>
“Jika suatu bender adalah bendera RI maka ada warna merah pada bendera tersebut”
Bentuk umum implikasi di atas adalah “p => q” dengan
p : Bendera RI
q : Bendera yang ada warna merahnya.
Dari implikasi diatas dapat dibentuk tiga implikasi lainnya yaitu :
1. KONVERS, yaitu q => p
Sehingga implikasi diatas menjadi :
“ Jika suatu bendera ada warna merahnya, maka bendera tersebut adalah bendera RI”.
2. INVERS, yaitu ~p => ~q
Sehingga implikasi diatas menjadi :
“ Jika suatu bendera bukan bendera RI, maka pada bendera tersebut tidak ada warna merahnya”.
3. KONTRAPOSISI, yaitu ~q => ~p
Sehingga implikasi di atas menjadi :
“ Jika suatu bendera tidak ada warna merahnya, maka bendera tersebut bukan bendera RI”.
Suatu hal yang penting dalam logika adalah kenyataan bahwa suatu implikasi selalu ekuivalen dengan kontraposisinya, akan tetapi tidak demikian halnya dengan invers dan konversnya.
contoh lainnya:
p: lumba-lumba adalah binatang mamalia
q: lumba-lumba adalah binatang menyusui
Implikasi:
jika lumba-lumba adalah binatang mamalia maka lumba-lumba adalah
binatang yang menyusui.
konvers:
invers :
jika lumba-lumba bukan binatang mamalia maka lumba-lumba bukan binatang menyusuikontraposisi:
jika lumba-lumba bukan binatang menusui maka lumba-lumba bukan binatang mamalia.Hal ini dapat dilihat dari tabel kebenaran berikut
p | q | ~p | ~q | implikasi p=>q | konvers q => p | invers ~p => ~q | kontraposisi ~q => ~p |
B | B | S | S | B | B | B | B |
B | S | S | B | S | B | B | S |
S | B | B | S | B | S | S | B |
S | S | B | B | B | B | B | B |
- not A adalah kebalikan dari premis A, dan
- not not A adalah kebalikan dari premis not A
Gallery Tabel Kebenaran Gerbang Logika
 Logika Bagian 1 Tabel Kebenaran Dan Gerbang Logika Dadan
Logika Bagian 1 Tabel Kebenaran Dan Gerbang Logika Dadan
 Gerbang Gerbang Dasar Logika Blog Pelajaran
Gerbang Gerbang Dasar Logika Blog Pelajaran
 Pengertian Gerbang Logika Dasar Dan Jenis Jenisnya
Pengertian Gerbang Logika Dasar Dan Jenis Jenisnya
 Rangkaian Logika Y Output A Input
Rangkaian Logika Y Output A Input
Macam Gerbang Logika Ajat Didik Budiansyah
Perencanaan Pembelajaran Rpp Ivon
 Buatlah Tabel Kebenaran Untuk Gerbang Logika Nand
Buatlah Tabel Kebenaran Untuk Gerbang Logika Nand
 Doc Gerbang Logika Eka Ashar Academia Edu
Doc Gerbang Logika Eka Ashar Academia Edu
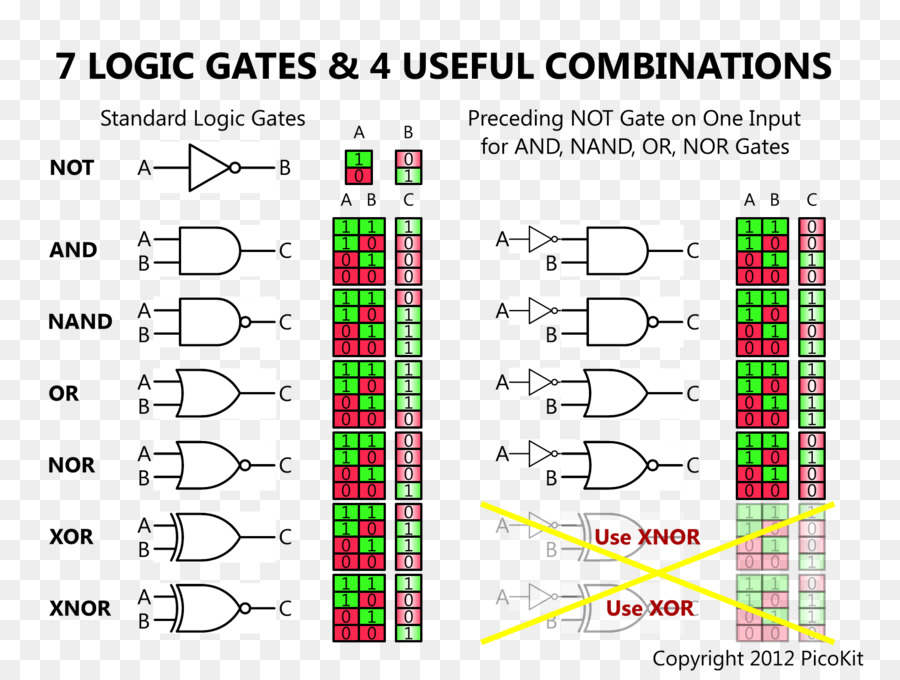 Gerbang Logika Dan Gerbang Tabel Kebenaran Gambar Png
Gerbang Logika Dan Gerbang Tabel Kebenaran Gambar Png
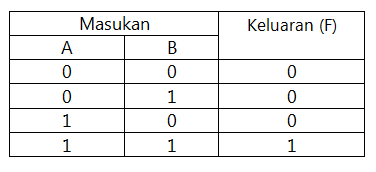 Gerbang Logika Dasar Maharadisjuanda Blog
Gerbang Logika Dasar Maharadisjuanda Blog
 Buatlah Tabel Kebenaran Untuk Gerbang And Dengan 3 Input
Buatlah Tabel Kebenaran Untuk Gerbang And Dengan 3 Input
Macam Gerbang Logika Ajat Didik Budiansyah
Gerbang Logika Tabel Kebenaran Dan Contoh Soal Sang Juara
 Pengertian Dan Macam Macam Rangkaian Pengolah Data Katakoala
Pengertian Dan Macam Macam Rangkaian Pengolah Data Katakoala
 Menentukan Tabel Kebenaran Dari Output Rangkaian Universal Gerbang Logika
Menentukan Tabel Kebenaran Dari Output Rangkaian Universal Gerbang Logika
 Dongan Blog Menentukan Ouput Tabel Kebenaran Pada Kombinasi
Dongan Blog Menentukan Ouput Tabel Kebenaran Pada Kombinasi
 Jenis Jenis Gerbang Logika Beserta Simbol Tabel Kebenaran
Jenis Jenis Gerbang Logika Beserta Simbol Tabel Kebenaran
 Gerbang Logika Not Pembelajaran Online Guru Elektronik
Gerbang Logika Not Pembelajaran Online Guru Elektronik
 Pengertian Dan Contoh Gerbang Logika Nand Not And Zikri
Pengertian Dan Contoh Gerbang Logika Nand Not And Zikri
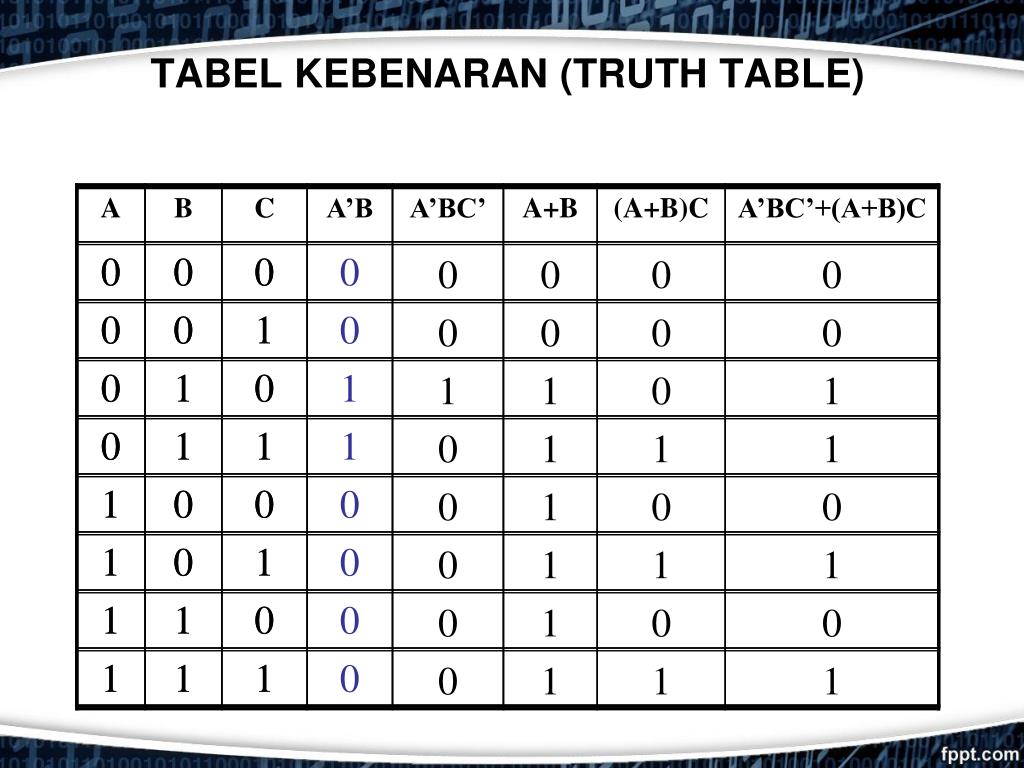 Ppt Elektronika Dan Instrumentasi Elektronika Digital 2
Ppt Elektronika Dan Instrumentasi Elektronika Digital 2


Comments
Post a Comment